

In this section, you will learn about concepts like moment, why Newtons are favored over Kilogram Force, how to select appropriate torque hinges that accomodate for torque variation and much more. By the end of this section, you will be able to understand how torque is calculated and why this is important when selecting a hinge. At the end, you will be introduced to Sasuga-kun, our special tool which not only calculates and simulates moment on a graph, it also links directly to appropriate products.
Moment is the tendency of a body to rotate about an axis due to applied forces. This calculation is critical for ensuring that torque hinges have the strength necessary to hold flaps and lids in place when the end users are no longer holding them.
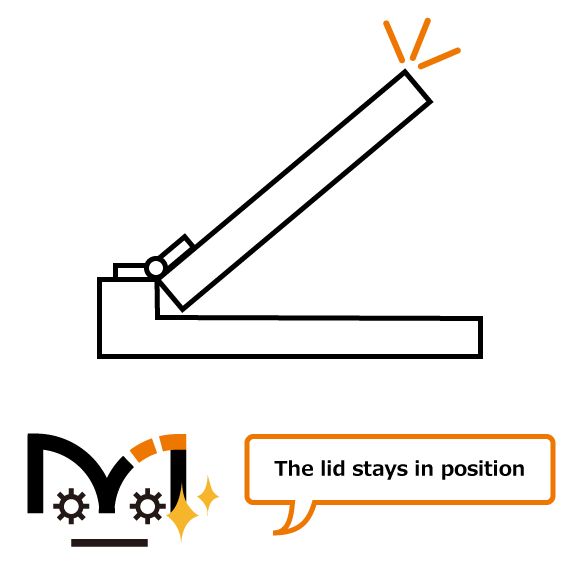
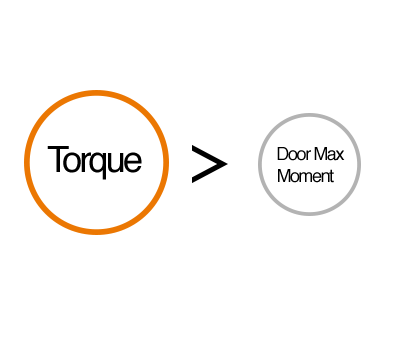
Door moment is the measure of the force of a door rotating around a hinge. When the hinge torque is higher than a door moment, it will stay in position.
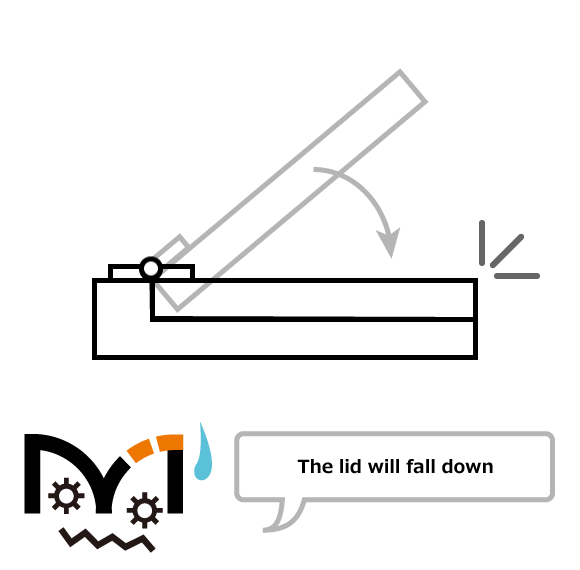

Until 1993, "kgf.cm" was used as a standard way to measuring units of torque and moment. After 1993, "N.m" has been used with more frequently partly because it is part of the ISO standard. It is also an SI unit, referring to the International System of Units. "Kgf.cm" is derived from gravitational force and will change according to local gravity.

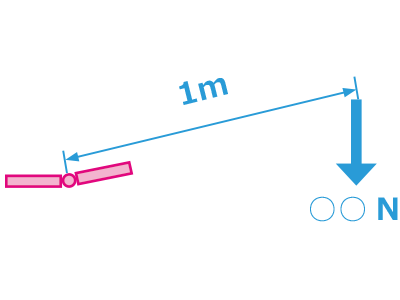
For instance, if the torque is 5N.m:
From the hinge axis, at a distance of 1 meter, if more than 5Ns of force is applied, the hinge will move.
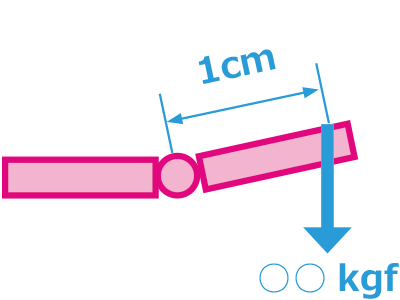
For instance, if the torque is 10kgf.cm:
From the hinge axis, at a distance of 1cm, if more than 10kgfs of force is applied, the hinge will move.
In order to a select a torque hinge, two things are necessary: the door maximum moment and the torque tolerance of the hinge.
The door moment is not constant as it rotates around an axis. If the torque hinge has a tolerance higher than the door moment, it will have free-stop. If it below the door maximum moment, it will not have reliable free-stop.

Torque hinges, have inherent variance in their torque tolerance. Which means that torque hinges have torque measurements that usually end with a ± and a percentage in order to indicate the possible range for the torque.

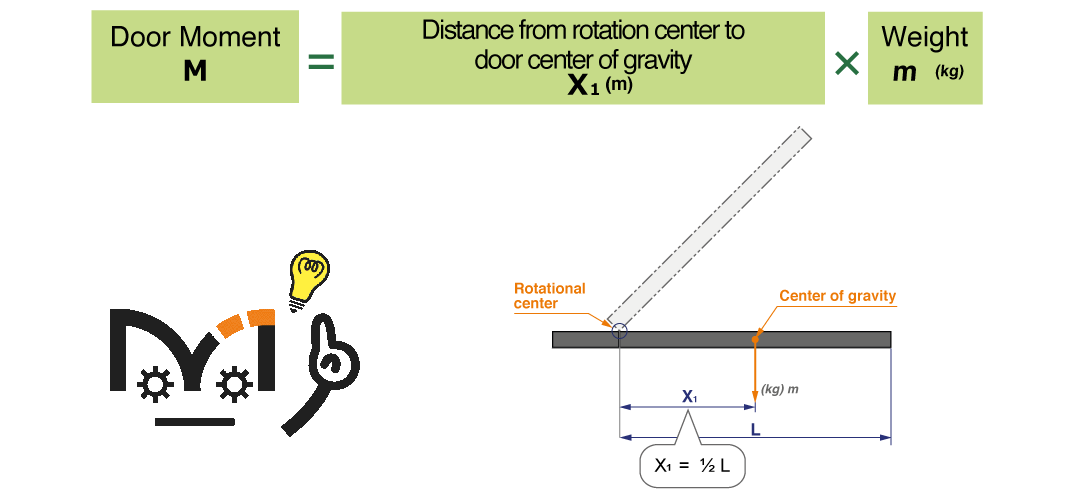
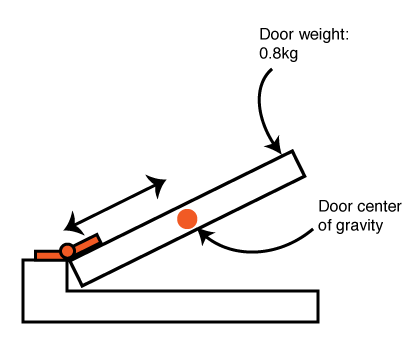
The maximum door moment can be calculated based on the center of gravity, along with the door weight.
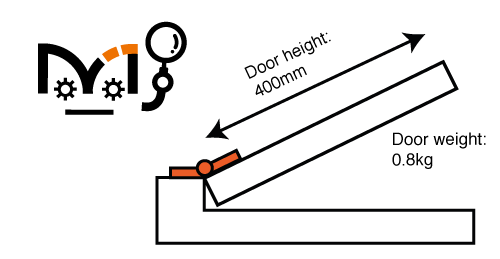
When installing two torque hinges with measurements like below (Door height of 400mm and weight of 0.8kg), which type of torque hinge would be most suitable if the torque tolerance range is 20%? (Assume that the door weight is equally balanced)
$$ M \ (Door \ moment) \ = X_1 \ (Distance \ in \ meters \ from \ rotation \ center \ to \ center \ of \ gravity ) \times m \ (weight \ kg) $$
$$ 0.2m \times \ 0.8kgf \times 9.80665 \approx 1.57N.m $$
Door maximum moment is 1.57N.m, which when divided by 2 ≈ 0.79N.m per hinge
Considering a door tolerance range of ±20%, the torque hinge that is the best fit is:
Torque hinge B with a torque strength of 1.0N.m per hinge.
At ±20%, the lower torque tolerance would be 0.8N.m, slightly more than is required
A professional use torque simulator with graphs and complex simulations in order to find best options for hinges. Using this tool will allow you to see tools vs moment graphs so you can identify the hinge that works best with your project.
Simply enter a few details from your project and this tool will provide you with a rough estimate of the torque involved in your project. Additionally, you can take those results and use them on our torque hinge page to find a product appropriate for the estimate.
This page contains a list of our torque hinge models. You can also enter torque to filter the torque values to find a product that falls within your range.